GET3DGS: Generate 3D Gaussians Based on Points Deformation Fields

Haochen Yu *

University of Science and Technology Beijing

Weixi Gong

University of Science and Technology Beijing

Jiansheng Chen

University of Science and Technology Beijing

Huimin Ma †

University of Science and Technology Beijing

TCSVT 2024

*First author, †Corresponding author

Paper Code arXiv

Abstract

The 3D Gaussian Splatting method has recently shown significant advancements in rendering speed and scene composition quality, enhancing its industrial applications and boosting the demand for 3D Gaussian asset generation. However, existing mature 3D generation technologies predominantly rely on implicit representations, which often struggle to balance geometric quality with editability. The production of 3D Gaussian assets generally involves diffusion models that require a dual-stage process of reconstruction and generation, resulting in substantial training and inference costs. To overcome these challenges, we introduce GET3DGS, an innovative approach that combines 3D-aware GANs with 3D Gaussian Splatting representations. This method facilitates the manipulation of the physical attributes of 3D Gaussians, such as geometry and texture, via point deformation fields. Offering faster inference speeds and end-to-end training capabilities, our model outperforms existing diffusion model-based methods. By deriving high-quality Gaussian point cloud geometric representations from 2D images, our approach reduces material accumulation costs and produces data compatible with 3D Gaussian rendering engines. We have evaluated the generative performance of our model on ShapeNet and OmniObject3D and demonstrate competitive results in terms of image and geometric quality relative to previous methods.

Figures

Use the figure component to display images, videos, equations, or any other element, with an optional caption.

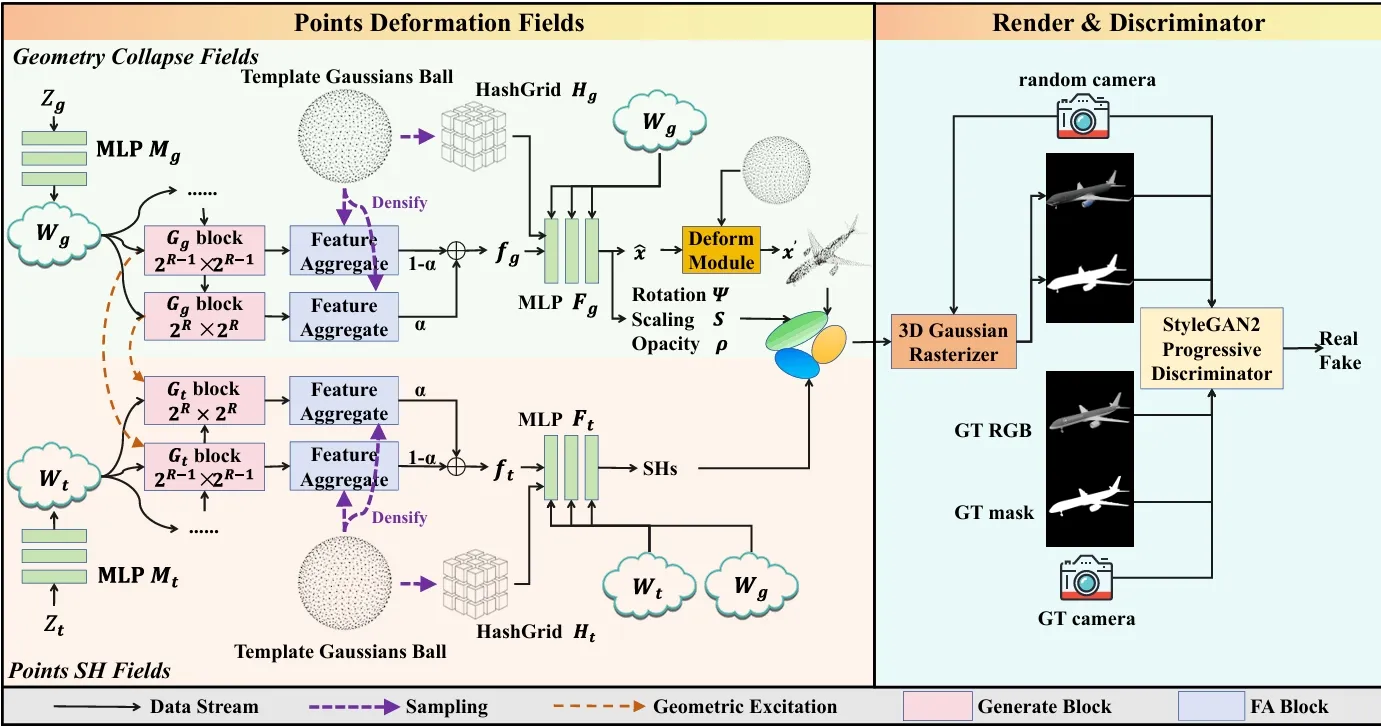
Diagram of the transformer deep learning architecture.
The main architecture diagram of our model GET3DGS, which is a 3D-aware GAN structure. The network includes geometry collapse fields and points SH fields. These two fields jointly constitute the points deformation fields. Both fields have generator blocks, feature aggregate modules, and an MLP decoder.

Methods

The geometry collapse fields are designed to map a template point cloud to a specific distribution, addressing the challenges of large solution spaces and unordered point cloud data. By introducing a strategy of density correction followed by radial collapse, the approach optimizes the solution space and point cloud density. This involves computing radial and rotational offsets in spherical coordinates, with the deformation function segmented into radial and rotational components. The method employs a feature aggregate module and a bi-plane structure for efficient feature utilization, enhancing network stability and rendering quality. The final representation integrates 3D Gaussian attributes, using activation functions to constrain physical attributes and prevent gradient instability.

CF([r,θ,φ],zg)=(r−r^zgr,θ+θ^zg⋅2π,φ+φ^zg⋅π)=(r,θ,φ)+(−r,2π,π)⋅diag(r^zg,θ^zg,φ^zg)\begin{aligned} CF&([r,\theta,\varphi],\mathbf{z}_{g})\\ &=(r-\hat{r}_{\mathbf{z}_{g}}r,\theta+\hat{\theta}_{\mathbf{z}_{g}}\cdot2\pi,\varphi+\hat{\varphi}_{\mathbf{z}_{g}}\cdot\pi)\\ &=(r,\theta,\varphi)+(-r,2\pi,\pi)\cdot diag(\hat{r}_{\mathbf{z}_{g}},\hat{\theta}_{\mathbf{z}_{g}},\hat{\varphi}_{\mathbf{z}_{g}}) \end{aligned}

The points SH fields are responsible for generating the texture of 3D Gaussians, utilizing a structure similar to the geometry collapse fields. Texture noise is encoded into a styled vector and processed through a textural generator block, with SH features generated on two planes to aid in shape coloring. Geometric excitation is applied by injecting intermediate features from the geometry collapse fields into the points SH fields, modulating the texture to adapt to the geometric distribution. This modulation ensures that texture features are influenced appropriately by geometry without being overwhelmed. The geometry and texture stylized vectors are concatenated to guide the MLP decoder in outputting texture attributes. The same sampling and aggregation methods used in geometry collapse fields are applied, allowing the learning of SH coefficients for effective texture representation.

SHs=SF(x⃗,zt,zg)=Ft(FA(Gt(Mt(zt),Gg(Mg(zg))),θ,φ),Mt(zt)⊕Mg(zg),Ht(x⃗)) \begin{aligned} SHs&=SF(\vec{x},\mathbf{z}_{t},\mathbf{z}_g) \\ &=F_{t}(FA(G_{t}(M_t(\mathbf{z}_t), G_{g}(M_g(\mathbf{z}_g))), \theta,\varphi),\\ &M_t(\mathbf{z}_t) \oplus M_g(\mathbf{z}_g), H_{t}(\vec{x})) \end{aligned}

Progressive densification training is a strategy designed to address the complexity of learning geometry and color mappings for large point clouds, especially when using GANs. This approach combines progressive generator resolution with the splitting of 3D Gaussians. Initially, a base resolution is set, and as training progresses, the resolution is doubled, allowing the model to densify by splitting coordinate positions. This method leverages the learnable rotation and scaling capabilities of Gaussian point clouds, ensuring training stability without reinitialization. At lower resolutions, fewer 3D Gaussians approximate the object’s basic structure and color, while high-resolution training refines these details. The process is mathematically described by progressively blending features from current and previous resolutions. Additionally, a Gaussian template is used to ensure uniform point distribution across a sphere’s surface, calculated using spherical coordinates. This template adapts to different resolutions by increasing point density, as detailed in the experimental configurations.

fgR(x⃗)=FA(GgR(Mg(zg),θ,φ)ftR(x⃗)=FA(GtR(Mt(zt),GgR(Mg(zg))),θ,φ)fgR(x⃗)=fgR(x⃗)⋅α+fgR−1(x⃗)⋅(1−α)ftR(x⃗)=ftR(x⃗)⋅α+ftR−1(x⃗)⋅(1−α) \begin{aligned} \mathbf{f}_g^{R}(\vec{x})&=FA(G_{g}^{R}(M_g(\mathbf{z}_g),\theta,\varphi)\\ \mathbf{f}_t^{R}(\vec{x})&=FA(G_{t}^{R}(M_t(\mathbf{z}_t),G_{g}^{R}(M_g(\mathbf{z}_g))),\theta,\varphi)\\ \mathbf{f}_g^{R}(\vec{x}) &= \mathbf{f}_g^{R}(\vec{x}) \cdot \alpha + \mathbf{f}_g^{R-1}(\vec{x}) \cdot (1-\alpha)\\ \mathbf{f}_t^{R}(\vec{x}) &= \mathbf{f}_t^{R}(\vec{x}) \cdot \alpha + \mathbf{f}_t^{R-1}(\vec{x}) \cdot (1-\alpha) \end{aligned}

Results

DatasetTypeModelFID↓KID↓(‰)COV↑(%)MMD↓
Car3DPointFlow--60.570.85
3DDiT-3D--31.702.98
3DDPM--60.240.95
3DPSF--70.731.03
3DMeshDiffusion--66.551.12
----------------------------------------------
2D→3DGET3D13.195.6644.130.80
2D→3DDiffTF73.2158.7249.531.36
2D→3DGaussianCube16.775.2261.480.90
2D→3DGET3DGS(ours)11.034.1766.971.04
------------------------------------------------------
Chair3DPointFlow--72.942.67
3DDiT-3D--76.832.82
3DDPM--81.732.87
3DPSF--81.922.65
3DMeshDiffusion--82.262.65
----------------------------------------------
2D→3DGET3D30.1618.3269.923.90
2D→3DDiffTF80.5665.3476.223.64
2D→3DGaussianCube32.1715.0663.393.60
2D→3DGET3DGS(ours)24.4113.6875.443.90
------------------------------------------------------
MotorBike3DPointFlow--64.570.88
3DDiT-3D--75.340.81
3DDPM--80.670.99
3DPSF--74.461.25
3DMeshDiffusion--89.041.08
----------------------------------------------
2D→3DGET3D74.0445.6665.751.74
2D→3DDiffTF102.4688.9541.026.05
2D→3DGaussianCube58.9530.0368.600.95
2D→3DGET3DGS(ours)61.1533.9881.250.92
------------------------------------------------------
OmniObject3D2D→3DGET3D28.9212.0131.216.34
2D→3DDiffTF93.8551.8834.596.05
2D→3DGaussianCube26.4511.1535.106.26
2D→3DGET3DGS(ours)26.2611.1332.596.46

Table: Evaluation of 2D image quality and 3D point cloud geometry quality under 512×512 resolution. The underlined values represent better geometric performance of the 3D baseline.

Visualization

BibTeX citation

    @ARTICLE{10777594,
  author={Yu, Haochen and Gong, Weixi and Chen, Jiansheng and Ma, Huimin},
  journal={IEEE Transactions on Circuits and Systems for Video Technology}, 
  title={GET3DGS: Generate 3D Gaussians Based on Points Deformation Fields}, 
  year={2024},
  volume={},
  number={},
  pages={1-1},
  keywords={Three-dimensional displays;Solid modeling;Training;Rendering (computer graphics);Deformation;Point cloud compression;Geometry;Image reconstruction;Shape;Image color analysis;3D Gaussian Splatting;3D generation;Differentiable rendering},
  doi={10.1109/TCSVT.2024.3511342}}